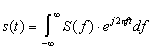
Darstellung im Frequenzbereich
In einem LTI-System kann nach FOURIER jedes beliebige Signal s(t) als nicht abzählbare unendliche Reihe von periodischen Elementarsignalen dargestellt werden. Mit den systemspezifischen Amplitudenfaktoren S(f) stellt sie sich in Form der Transformationsgleichung, auch inverse FOURIER-Transformation genannt, dar:
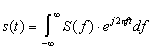
Somit stehen für die Darstellung neben dem Zeitbild auch die Funktion der Amplitude S(f) in Abhängigkeit der Frequenz, das sog. Amplitudendichtespektrum und die Funktion des Phasenwinkels j (f) = 2p ft in Abhängigkeit Frequenz, der sog. Phasengang zur Verfügung.
Da das Amplitudendichtespektrum alleine keinerlei zeitliche Angaben enthält, hat es nur für stationäre bzw. quasistationäre Vorgänge eine Aussagekraft. Dennoch liefert es wichtige Auskünfte z.B. über bestimmte klangliche Eigenschaften, u.a. wie hell, dunkel, hoch oder tief, auch Grundtöne und Formanten können, sofern vorhanden, gut erkannt werden.
Ebenso kann der Phasengang wichtige Informationen beinhalten, besonders für die Übertragungstechnik, sind doch starke Phasenfehler in Form von Artefakten nachweislich hörbar.
Heute werden Spektren mit Hilfe Rechnergestützter FFT-Analysatoren (Fast-Fourier-Transformation) gewonnen. Die FFT ist eine Form der diskreten Fourier-Transformation (DFT), die die Abtastung der Meßsignale im Zeit- und Frequenzbereich kombiniert. Durch eine geeignete Fensterung (das Zeitsignal wird dann als periodisch mit der Fensterbreite als Periode angenommen) wird auch der Frequenzbereich bei der DFT diskret. Das Problem der Fensterung ergibt sich immer dann, wenn das Spektrum eines aperiodischen Signals mit Hilfe der DFT geschätzt werden soll. Das Spektrum eines periodischen, diskreten Signals ist ebenfalls periodisch und diskret. Dadurch wird aus dem Fourierintegral eine Summe.

So kommt es zu Verfälschungen in der Amplitudendichte (Seitenschwingungen) durch die Einschränkung auf ein Zeitintervall. Mildern können dies Fensterfunktionen wie z.B. Hamming und Kaiser-Bessel, die die Seitenschwingungen bedämpfen. Gleichzeitig werden dadurch aber auch im Fenster liegende Frequenzkomponenten breiter. Hinzu kommt, daß je kürzer ein Klangbeispiel gewählt wird, desto ungenauer ist die Frequenzauflösung und umgekehrt. So sind die Abtastwerte, die durch die Einstellung der Fensterbreite fest gegeben sind, umgekehrt proportional zu der Frequenzauflösung. Dieser Zusammenhang besteht auch bei der klassischen Bandfilteranalyse (Küpfmüller'sche Unschärferelation). Dies wirkt sich daher besonders kritisch im unteren Frequenzbereich aus.